Adjusting game score for D1 men's college hockey

An adaptation to make the formula appropriately weighted for men's college hockey

Welcome to Fresh Ice, a data-driven college hockey newsletter. Each week, I’ll be publishing fresh (no pun intended) content that focuses on educating and explaining all aspects of the game. Haven’t subscribed yet?

---

In 2016, Dom Luszczyszyn introduced a metric called game score, which is intended to provide a single number that approximates a player’s performance in a given game. In that original story, he included the formula for the metric and how he arrived at it, so it’s inspired various adaptations since then.

Shawn Ferris adapted a version for the NWHL in 2018, and Mike Murphy did the same as part of a two-part series on examining player development in NCAA D1 women’s hockey in June. But to my knowledge (and please, please correct me if I’m wrong on this — I searched high and low but very easily could’ve missed something!) no one has adapted it to D1 men’s hockey, so I decided to investigate it.

Many disclaimers apply here, so I want to make sure they’re all clear from the beginning. One, I am what you could call technologically illiterate, so I could not and did not gather my own data for this. I worked with box scores and data available from Pick 224, which for the most part doesn’t include shots on goal, blocked shots or faceoffs. I’ll explain why that matters further down, but just keep that in mind.

Second, game score is a great metric for approximating a player’s performance, but it’s just that — an approximation. Especially because I manually entered all the data from the box scores, there could be a mistake that affects a player’s score from a given game.

Method

Here’s where I tell you that this is actually the second iteration of this project. Back in February, I created a spreadsheet inspired by Alison Lukan’s player tracking spreadsheet to keep track of Michigan’s man games lost to injury this season.

Looking at all the blank spaces, I thought it could be interesting to add in a game score for each player in each game, much like Alison does. In Dom’s original formula, there are numerous statistical categories like penalties drawn and Corsi for and against that aren’t available in college hockey. For my first version of this sheet, I just left those out but left the weights on each stat the same as when Dom did it.

For clarity’s sake, this was my original formula after removing stats I didn’t have access to from Dom’s: Player Game Score = (0.75*G)+(0.7*A1)+(0.55*A2)+(0.075*SOG)+(0.05*BLK)+(0.01*FOW)–(0.01*FOL)+(0.15*GF)–(0.15*GA)

That gave me a pretty decent approximation and served my purposes well enough. All I wanted was a quick, at-a-glance metric that would tell me which players played well and which didn’t, and it did just fine for that.

But after reading Mike’s work earlier this summer, I realized I could refine things and make it more applicable to men’s college hockey.

Following Mike’s methodology pretty closely, I pulled data from Pick 224 that covered the last five years of men’s college hockey. Using that data, I was able to weight goals, primary assists and secondary assists according to their frequency to goals. For example, there were 6,991 even strength goals scored from 2016-2020 and there were 6,664 primary assists, which gives us a factor of 0.953 for primary assists.

The data did not include blocked shots, faceoffs or shots on goal, and because those had relatively low weight in Dom’s formula, I left those the same.

I also followed Shawn’s method from his NWHL game score work and used league-wide power-play percentage to weight the impact of taking a penalty.

Dom scaled his formula down 75% to make the game scores roughly equivalent to points so people would be familiar with what the game score represented, and I kept to that methodology here because I used some of the same weights he did. Also keep in mind that the goals for and goals against are just goals scored at even strength — it does not include special teams, empty-net or extra-attacker goals.

That left me with this formula: Player Game Score = (G*0.75)+(A1*0.715)+(A2*0.555)+(SOG*0.075)+(BLK*0.05)+(FOW*0.01)-(FOL*0.01)+(GF*0.15)-(GA*0.15)-(PNT*0.138)

I’m realizing as I write this that the weights for primary and secondary assists are nearly identical to the weights in Dom’s formula, so I may have wrangled with Excel for nothing, but at least now I know I have appropriate weights for college hockey and I’m not just hoping the NHL formula applies.

Testing

Remember when I said I’m technologically illiterate? Statistics isn’t really my thing, either. For that reason, and others, I didn’t put this formula through much testing. Most of the testing consisted of looking at the scores from each game and seeing if they seemed like they made sense, which they did.

I’ll also add that because I essentially followed the exact methodology from three versions of this formula that did test well and appear to be accurate, I didn’t feel a lot of pressure to do the same here. If I royally screwed something up, it would’ve been borne out in the final scores making little sense, and that didn’t happen.

However, if someone who is good at computers and statistics would like to help me see if this adaptation genuinely works or expand upon it, I’m all ears. My email is bajohn@umich.edu or my Twitter DMs are open!

Results and thoughts

After finalizing the formula, I applied it to this season’s games in the same way I did with the first, halfway done version back in February. I plan to do some fun stuff with these numbers in a few upcoming stories (hint: it’ll have something to do with certain players’ best and most average games) but for now, let’s take a macro look.

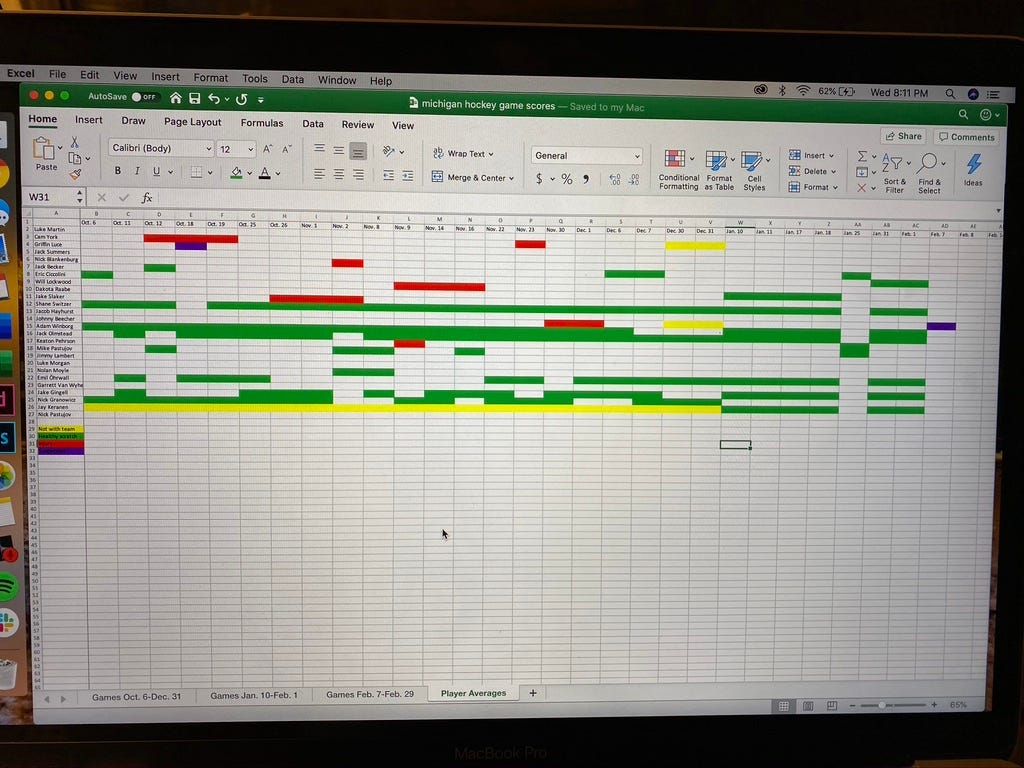
Here’s the spreadsheet with every score (and fun color-coding!) A prize to anyone who guesses what each color means, and feel free to play around with it as you see fit. Note that I only included players who appeared in 15 or more games, mostly because the others only played in a handful of games and their averages are pretty skewed by small sample size.

The games that are labeled in red have incomplete data. Specifically, these games are missing blocked shots.

I find the colored lines very pleasing in a weird way. Again, big shoutout to Alison for the spreadsheet inspo!

One of the things I like best about game score is while most of the time the highest-rated player also led the team in points, sometimes it makes me stop and realize something I paid less attention to had a bigger impact than I thought. Michigan’s 8-4 win over Wisconsin in February is a great example.

Nick Granowicz had his first career hat trick, but finished with a game score of 2.875 because he only took three shots and was on the ice for a goal against in addition to his three goals for, which brought down his score a little.

Slaker, on the other hand, tallied the season’s highest game score at 4.004 because he scored one goal, had three primary assists, took seven shots on net and was on the ice for four of Michigan’s goals — and no goals for Wisconsin. That particular instance was a good reminder for me that because primary assists are weighted almost as heavily as goals, a player that has an excellent night as a facilitator can come away with the team’s best game score.

On a team-wide level, it’s no secret that Michigan’s offense started the season pretty slowly. That comes out in the average game scores, too, as no player finished with an average game score above 1. Slaker came closest, at 0.874, which makes sense as he led the team in scoring. However, if you include players who appeared in less than 15 games, Slaker is dethroned, and I’ll Venmo $5 to anyone who guesses who it was.

I also want to add that game score isn’t a perfect metric, but it is a pretty good one. The impact of special teams isn’t accounted for, and if Dom couldn’t figure out a way to include it, I don’t like my odds of figuring it out either. It also is heavily weighted toward scoring stats, so the impact of defensemen — particularly stay-at-home defensemen — is somewhat lost. That ties into a larger question in analytics of how to measure defense when good defense can really be considered the absence of events, but I won’t bore you with my thoughts on that right now.

Overall, it’s a good metric that gives a simple, accessible understanding of how a player performed on a given night, and I find that valuable.

---

I hope this leaves you with an understanding of what game score is, how it’s calculated, and how it can apply to college hockey. Up next, I’ll be taking these scores and doing some pretty fun things with individual player data, so stay tuned for that!